How to Know Which U to Use in Substitution Method

The substitution in this case would be u 2 cos 1 x d u sin 1 x d x sin 1 x d x d u u 2 cos 1 x d u sin 1 x d x sin 1 x d x d u. E u C e x 2 2x3 C.

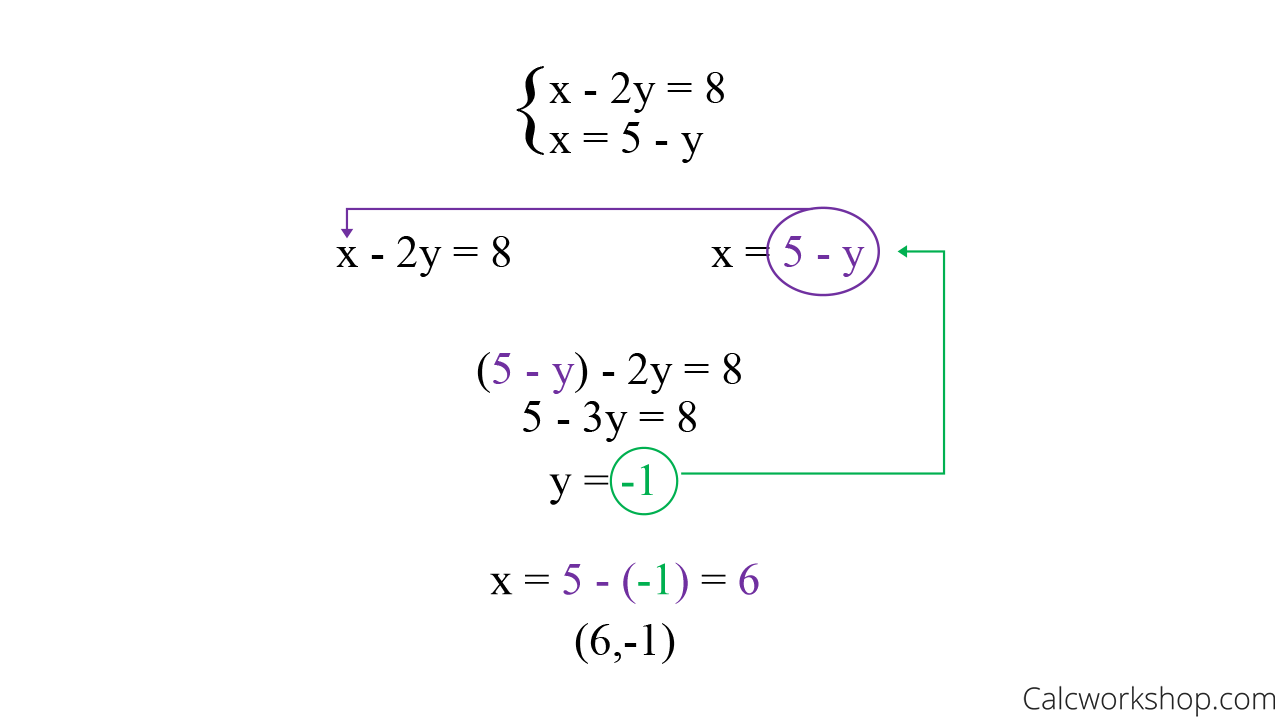
What Is The Substitution Method Just 3 Simple Steps

Using u-substitution makes it easier to read and simplify composite functions which can otherwise start to look messy and intimidating.

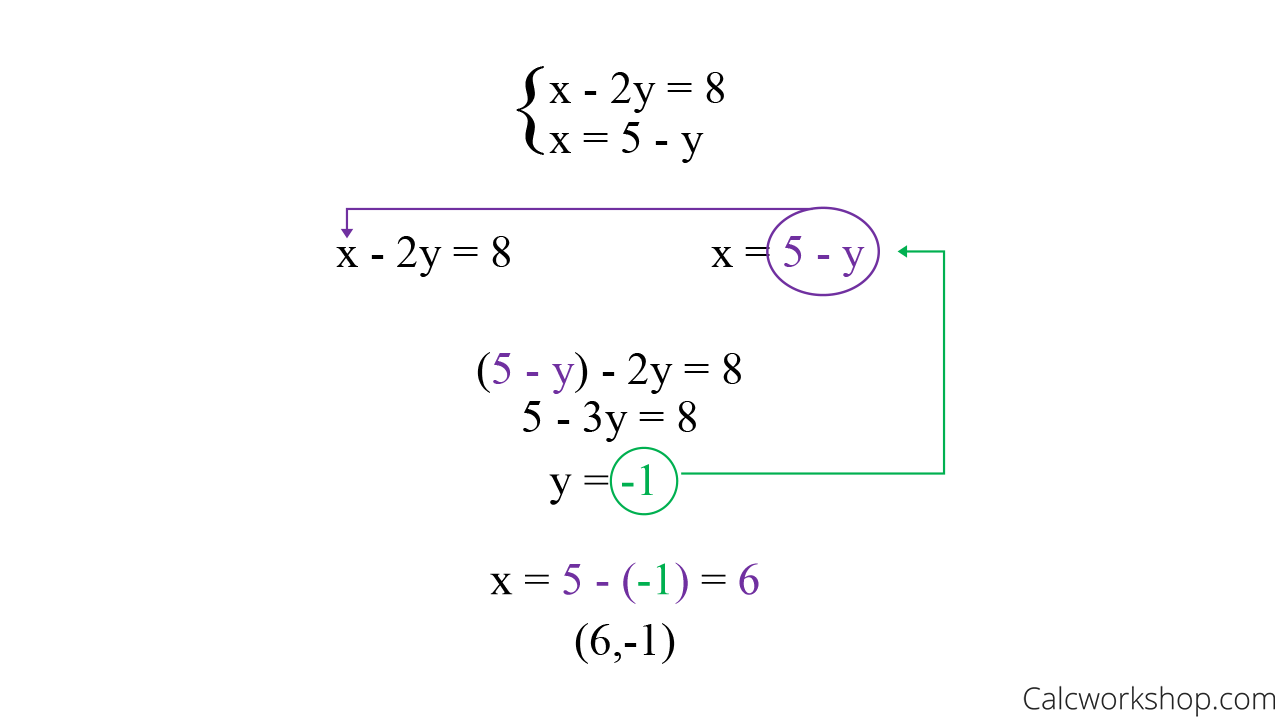
. Solve one of the equations for either x or y. Letting be or will never work. That is if you have f g x g x d x use a u-sub.

Then must be defined as. It explains how to integrate using u-substitution. Here is another illustraion of u-substitution.

This method is also called u-substitutionThe idea behind doing u-substitution is to rewrite the integral into a form that easily fits with the known rules of integrals. Substitute plug-in this expression into the other equation and solve. Of course it is the same answer that we got before using the chain rule backwards.

Cos u du sin u C. Carefully select whether you want to evaluate u substitution functions as per definite integral or indefinite integral. Since it doesnt factor and the coefficient on the 1st degree term is odd you might as well just use the quadratic formula.

Now you need to substitute plug-in. You will get two answers just like you always do when you solve a quadratic. Well I knew it would.

We will take two examples to understand it in better way. In this case we can set u equal to the function and. That is if you have fgxgxdx use a u-sub.

Suppose we are using the binary search technique. First dont forget to correctly deal with the. The first step is to isolate one of the variables x or y in one of the equations.

U14 l2 t1 we1 Substitution Method. If that is present at middle then the algorithm terminates otherwise we take. So with this substitution well be able to rewrite the original differential equation as a new separable differential equation that we can solve.

Then we will make a suitable substitution that will simplify our integrand so that we can integrate as illustrated in three easy steps below. In this technique we check whether the element is present at the end or not. Solve this new equation for x.

Substitution method review systems of equations CCSSMath. That way you know that that variable is equal to everything on the other side of the equals sign from it. Cos x 2 2x dx.

In this case they will be real but irrational. Using u-substitution we substitute u g x u gx u g x and d u g x du gx d u g x into our integrand which undoes the chain rule. Solve the equation in just like any other quadratic.

Steps for Using the Substitution Method in order to Solve Systems of Equations. Solve for the second variable. And finally put ux2 back again.

Plugging this into the differential equation gives 1 bv a Gv v abGv dv a bGv dx 1 b v a G v v a b G v d v a b G v d x. First you need to solve one equation for one of the variables. The basic method for using U-substitution to perform definite integral substitution and appropriately change the bounds of the.

We can now easily put the value of y in any of the given equations to find x. Let u x 3 3x. Once you have your two expressions for the.

Identifying the Change of Variables for U-Substitution Well the key is to find the outside function and the inside function where the outside function is the derivative of the inside function. A u-sub can be done whenever you have something containing a function well call this g and that something is multiplied by the derivative of g. That worked out really nicely.

The first step of using this u substitution calculator is to select the function from the dropdown or enter the function manually. If you cannot consider integration by parts. Here we will see how to use substitution method to solve recurrence relations.

The substitution method also called u substitution is used when an integral contains some function and its derivative. You need to determine wh. Substitute your answer into.

Assume we have a system of equations with 2 equations and 2 variables the simplest system we could have N equations and N. So cos x2 2x dx sin x2 C. A u -sub can be done whenever you have something containing a function well call this g and that something is multiplied by the derivative of g.

Since the coefficient of y in equation 2 is -1 it is easiest to solve for y in equation 2. Put in y or x form Substitute this expression into the other equation and solve for the missing variable. Integration by parts is whenever you have two functions multiplied together--one that you can integrate.

F g x g x d x f u d u int fgxgxdx int fudu f g x g x d x f u d u. Now at first glance this may seem complicated but Ive got some helpful tricks for keeping things straight. Two things to note here.

This article reviews the technique with multiple examples. Resubstitute the value into the original equation to find the corresponding variable. This calculus video tutorial provides a basic introduction into u-substitution.

There is no real rule to decide which variable to isolate you just isolate the easier oneOr in the cases where you want to solve the system for only one variable you need to isolate the other. Solve one equation for one of the variables. Always do a u -sub if you can.

Then Go directly to the du part du 3x 2 3 dx 3x 2 1 dx so that 13 du x 2 1 dx. You can then take that whole side and substitute it into the other equation where the variable you isolated originally was. Solving a system of equations by substitution.

Sin x 2 C. Suppose we know that integral from 0 to 5 of f. Solve 1 equation for 1 variable.

Choosing the wrong expression for will result in a wrong answer. For -substitution to apply we must be able to write the integrand as. The method of substitution involves three steps.

We know from above that it is in the right form to do the substitution. For example in Problem set 1 must be defined as. The substitution method is a technique for solving a system of equations.

In essence the method of u-substitution is a way to recognize the antiderivative of a chain rule derivative. Substitute the solution from step 1 into the second equation.

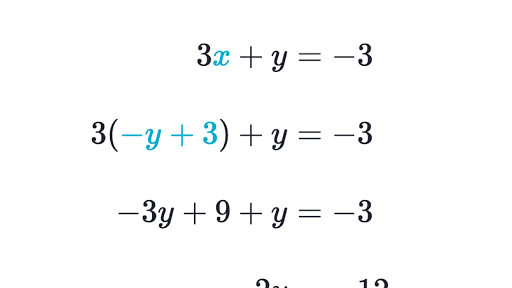
Substitution Method Review Systems Of Equations Article Khan Academy

Substitution Method Definition Steps Examples

Substitution Method